Since the beginning of the application of Artificial Intelligence to Big Data, and the availability of Artificial Intelligence Based tools in the Cloud, I heard every possible statement and its contrary about what these new tools can do! I am among the ones that more than 20 years ago started applying Artificial Intelligence to the solution of commercial problems, and in particular to financial analysis, so I know what can actually be done and with which tools and techniques it can be done. Therefore, I quickly realized that the recent revival of artificial intelligence techniques was affected by a large amount of misinformation.
This article is a classification of artificial intelligence techniques and a discussion of which of them may benefit from the Cloud, and/or may be applied to data science and to the analysis of big data. It was conceived as an initial guide for mangers and/or professionals that would like to adopt some of these new technologies to solve their problems.
What changed in Artificial intelligence in the last 20 years?
Basically, nothing! At least in the algorithmic theories behind the various artificial intelligence techniques. For sure, new applications of existing theories, and minor refinements, but mainly more computational power! That’s why Cloud and Big Data come in! That’s why the cloud triggered this revival or artificial intelligence.
Actually, a renewed interest in neural networks started when video cards gave the possibility to customize the operations performed on each pixel by providing chunks of code called “pixel shaders”. The initial purpose was empowering 3D rendering with photo-realistic effects and special effects, but in a short time developers realized that video card were actually powerful processors capable of executing single instructions (the one provided by pixel shaders) in parallel on millions of data (all pixels). Actually they are SIMD (Single Instruction Multiple Data) parallel machines. Exactly, what is needed to simulate neural networks where the same “neuron simulation” instructions must be executed on all simulated neurons, simultaneously. As a consequence most of video card producers started building “special video cards” to be used as SIMD machines, that are the ones used in the cloud to simulate neural networks and to perform statistical computations on big amount of data.
New kind of SIMD machine were conceived and are used in famous clouds, but this great progress just involves SIMD machines. No commercial MIMD(Multiple Instruction Multiple Data) machine capable of executing trillions of different chunks of code on different data has been conceived, so big parallelism is available only if exactly the same instruction must be executed on big amounts of data. The main difficult with massive parallel MIMD machines are communications among millions of executing software chunks and their assignment to idle processors.
Accordingly, neural networks and statistical computations that may benefit from SIMD machines are the artificial intelligence battle horse that comes with various famous clouds! In fact, other artificial intelligence techniques that I am going to describe in this post would require MIMD machines to gain benefit from the computational power offered by the cloud. Notwithstanding this, you may find services based on them that some companies offer in the cloud to take advantage of the SaaS (Software as a Service) model and scalability offered by the cloud, instead of the SIMD massive computational power.
In the next sections I’ll discuss the main artificial intelligence techniques, and their applications.
Artificial Intelligence basic techniques.
AI techniques may be split into three categories: perception, symbolic reasoning, and learning. In this section we will cover just perception and symbolic reasoning techniques, since learning is discussed in a dedicated section.
When, you remember facts, or plan a journey, you don’t think to about all details of all paces, you don’t remember or imagine all pixels your eyes have seen or will see. Actually, you don’t think at all to pixels. In fact you brain wouldn’t be able to store and process pixel level information, so it extracts just some relevant facts in symbolic format. When you look at a scene, you recognize all objects in the scene, attach some features to them like color and dimensions and their position in the space. In other terms you map millions of pixels into a few kilobytes of concepts, and attach some attributes to them. For instance: chair (brown, average dimension, next to the table, on the left side of the table), table (….),….
The mapping of raw data into concepts is called perception, and it is the most difficult problem of artificial intelligence, since it requires an a priori knowledge about all concepts, properties and typical appearances. In general, perception is not a stand-alone process but it interacts with higher level reasoning components to disambiguate alternative interpretations of input data. Perception is involved in image recognition, and speech understanding.
Perception is based on two important concepts: features extraction, and pattern recognition. I’ll use image processing to explain this two concepts, but they apply to any kind of perception. Feature extraction is a numerical pre-processing of the input data. Typically, images are pre-processed to extract object boundaries with edge detection algorithms, to extract information of surface orientation (shape from shading, and other shape from x techniques), and so on. Then, pattern recognition is applied to any result of previous pre-processing and to the original data. Pattern recognition looks for “typical patterns” on the input data that may give information on the objects involved. For example you may recognize typical parts of objects. Pattern recognition is a recursive process: in turn recognized patterns are be combined into higher level patterns till the final objects are recognized.
Feature extraction is usually performed with mathematical techniques (gradient and partial derivative computation, for instance). However, in order to take advantage of SIMD machine computational power, and of learning techniques, they may be performed also by specialized neural network whose topology is designed to mimic the the needed mathematical operations.
Pattern recognition, is where neural networks performs better! Neural networks may be “trained” to recognize patterns (such as phonemes in speech recognition). Neural networks learning techniques are also able to guess automatically what patterns are useful in a perception task (multi-level hierarchical networks). Pattern recognition may be performed also with other techniques that mix mathematical computation and symbolic reasoning and use complex learning algorithms. However, the computational power available on SIMD machines in the cloud made neural network the best approach to pattern recognition, at least in the recursive levels closer to raw data.
Once we have relevant symbolic data extracted from raw data we may apply several symbolic reasoning techniques:
- Heuristic search tries to find a solution to a problem by exploring all possibilities with the help of an heuristic function that selects the most promising options. Among the various search techniques alpha-beta search is used for playing games against an human adversary (chess machines, for instance). alpha-beta search looks at the best “move”, trying to forecast the best “moves” of the human adversary in the search. More complex search techniques, use “constraint propagation” and “least commitment” to cut the search tree. Constraint propagation, uses constraints imposed by a choice to cut further choices, while “least commitment” tries to delay choices till constraints coming from other choices make them univocal.
- Planning. A planning module has a description of its environment and it is required to achieve a certain goal by selecting a sequence of actions taken from a set of possible actions. Each action describes pre-requisite for the action to be possible and the effect of the action. There are efficient planning algorithms that work under the hypothesis that the external environment changes only for the actions of the planning module. Cases where also external causes may change the environment can be dealt with by re-computing the plan after each action. Cases where an adversary modifies the environment to hinder the plan can’t be faced with these algorithms, since re-planning after each action might result in an endless loop of actions that don’t achieve the goal. Planning against adversaries may be faced either with alpha-beta search, or, in more complex cases, with multi-agent reasoning (see below). Typical applications of planning include automatic syntheses of software, robot planning, and implementation of characters in video-games.
- Rule based systems apply rules for inferring facts from a pre-existing knowledge base and input data. Rules have pre-conditions that are verified on the the already known facts, with a process known as “pattern matching” that at the same time verifies the applicability of the rule and instantiate some variables that adapt the rule at the specific situation. There are efficient algorithms and indexing techniques to select all applicable rules and to order them according to pre-defined priority criteria. Typical applications are automatic theorem proving, and decision systems.
- Belief revision systems (also called truth maintenance systems), are “facts” databases where each fact is recorded together with the chain of facts used to infer it, that is with its justifications. Therefore, when we remove a fact all consequences are removed too, and when we re-assert it all its previously computed consequences are re-asserted again, thus allowing “what if…?” analyses. For instance, if during a search for a solution a problem solver passes again through an already analyze hypothesis in a different node of the search tree, then all its consequences re-appears with no further computational effort.
While belief revision systems may be used to speed up problem solving in general, their main applications are automatic diagnosis systems, that analyze all consequences of assumptions (faults) to explain the misbehavior of devices. All hypotheses (for instance all possible faults), with their consequences may be analyzed either sequentially, or in parallel through complex logic operations performed on sets of several hypotheses (see De Kleer, Assumption Based truth Maintenance System). - Multi-agent reasoning systems are rule based systems capable of reasoning about other agents’ beliefs. They are able to cooperate and coordinate with other independent systems and to fight against adversaries. They are used in robotics (coordination with other robots or humans), intelligent weapons (autonomous fighting droids, for instance), video games, and in simulation of conflicts among human agents (war games, economic simulations, etc.).
- Spatial and time reasoning, is a set of techniques that mix pure mathematical and geometrical algorithms with other artificial intelligence specific techniques like planning, and rule based reasoning. For instance, geometrical reasoning is involved in robot planning and videogames to let agents insert trajectories planning in their “symbolic plans”. Trajectory, planning is performed with computational geometry algorithms whose application is orchestrated by artificial intelligence modules.
- Neural networks are used by “neural networks fans” also in symbolic reasoning as an alternative to rule based systems, with the justification that human symbolic reasoning is performed with neurons. However, this argument is quite poor since, neurons are for the human brain what transistors and CMOS are for computers, but none asserts that building general purpose CMOS or transistors nets is better than writing software. As a matter of facts it is difficult to represent complex facts with attributes in a neural network, so there is no advantage in using them instead of rule based systems. As discussed at the beginning of the section, it is easy to represent “raw data” and “patterns in raw data” in neural networks, so they perform great basically in “pattern recognition”.
It is worth to point out the practical differences between” pattern recognition” and “decision making”. From one side pattern recognition is a particular case of decision making, and on the other side one might use pattern recognition to take decisions.
In general, decision making systems contain “rule based systems” modules and involve the application of general rules, that are “instantiated” to fit them to any specific situation. Instantiation is a process similar to assigning values to the formal parameters of a procedure. Let do a simple example to clarify. Suppose we have a fact saying “John is an human”, and that we have a rule saying: “If x is human then it is mortal”. “x” is a kind of formal parameter that may be substituted by any actual value, such as “John”. So the result of the instantiation is “if john is human then it is mortal”. Applying the instantiated rule to our fact “John is human” we get a new fact: “John is mortal”.
On the other side “pattern recognition” usually do not use “general rules” and variables to be instantiated, at least in the very general form we have seen for “rule based systems”. Their rules are about specific “patterns” they try to recognize. Where each pattern may have a finite and small set of appearances. The only kind of generalization allowed are continuous deformations of the allowed appearances. A typical pattern recognition task is the recognition of handwritten characters. For each character there are a few ways to write it, but a lot of “possible deformation” of each of them. The “0” character has just one way to be written, but the basic “0” may be “deformated” in several ways: by changing its width, its height, allowing various kind of asymmetries, etc.
Another way of “adapting” a pattern recognition rule is by applying it in a specific place of time and space. For instance a handwritten character recognition routine may be applied to various area of an image to look for a character in that area. As a matter of fact, in image recognition, pattern rules are moved along the two dimensions of the image.
Since, neural networks while having no concept of variable instantiation, are good in “learning” possible “deformations” they perform well in pattern recognition. Spatial and time translations are achieved by using special kinds of networks called “convolutional networks”.
Pattern recognition based on neural networks may be used in the early stages of analysis and decision making systems, to extract relevant patterns form raw data. Typically pattern recognition and mathematical computations extracts “relevant facts” about data, then these “relevant facts” are processed by “rule based systems” to get either final decisions or human understandable analyses. Basically, this is the way artificial intelligence techniques are applied to “Data Science” and Big Data.
Neural networks basics.
A neural network is a networks whose nodes are connected by directed edges having numeric weights. Each node has input edges and an output that may be connected to the input edges of other nodes, or acts as a final output value.
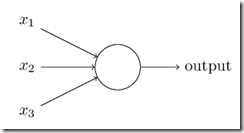
The output of a node is computed as a function of all values received by its input edges, their weights and a threshold associated to the node:
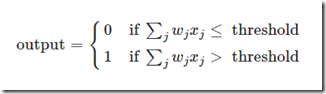
The above equation may be rewritten in compact notation as (we called “b” the threshold):
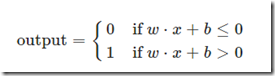
or using the step function “u”:
output=u(w.x+b)
Where “u” is the step function:
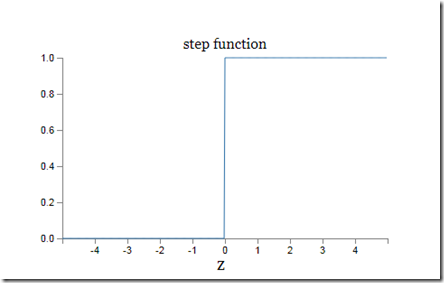
Neural networks based on the step functions are called “perceptrons”. However, since during learning neural network must be processed by mathematical optimization algorithms that work only with “smooth” functions the step function, that is discontinuous (i.e. not smooth), is substituted by a “smooth” variant, the sigmoid function:
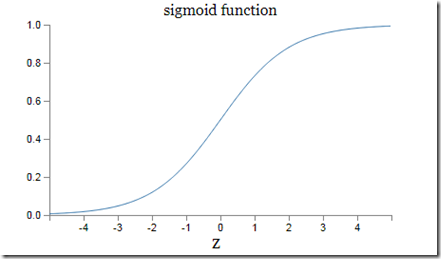
With this modification node equations become:
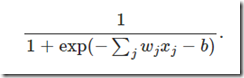
Standard neural networks are organized in layers where each node of a layer has input edges coming from all nodes of the previous layer. Below a three layers network:
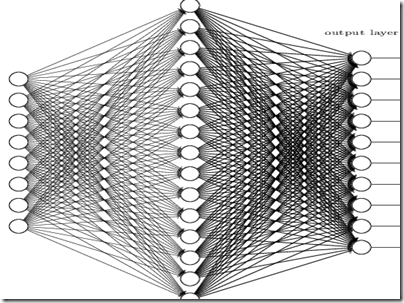
The first layer contains all input nodes, while the last layer contains all final output nodes. All internal layers are called hidden layers since they don’t communicate with the external environment. Complete connections among levels ensures completeness and generality of the network. Then the network is adapted to a specific problem by computing all its parameters (thresholds and weights) with “learning algorithms” (see next section).
The networks should be able to interpolate any function once they have been trained with enough examples. It can be proved mathematically that 3 layers networks are able to approximate any continuous function with a precision that can be increased with no limits by increasing the number of the hidden layer nodes, and by adequately choosing its parameters. That is why neural networks are so good in pattern matching: they interpolate the function that recognize all “deformed” variants of the finite sets of appearances a pattern may have.
Notwithstanding the previous completeness theorem, in practice, 3 layers networks do not perform well in complex problems, since complex problems would require a number of hidden nodes and training examples that grows exponentially with the complexity of the problem to cope with the exponentially growing possible combination of inputs that might get the same result. For instance if we would like to recognize an handwritten character that may appear in any position of an image we must supply example of all variants of that character with several “deformations” in all position it might have in the image. Moreover, we need an exponentially growing number of hidden nodes to encode the complexity of the resulting function. As a matter of fact exponentially growing problems can’t be dealt with, no matter how much computation power we have, since increases in the size of the problem would eventually saturate any computational power.
Software typically copes with complexity by using hierarchical decomposition of tasks. Lower level routines performs common useful tasks and furnish input to higher level modules in a recursive fashion till the whole software has been decomposed hierarchically. In the example of image recognition lower level modules performs what we called features extraction, then simple patterns are recognized, then patterns are grouped into higher level patterns, till a whole object is recognized. This lead us to analyze multilayer networks. In fact, we might use networks with several layers and train them so that the various layers needed in image recognition are learned automatically by using standard neural network learning algorithms:
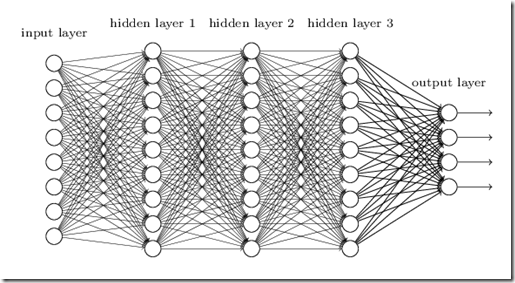
Unluckily, automatically learning a whole processing hierarchy without any heuristic, and/or a priori knowledge is itself an exponentially complex problem, so it can’t be solved in practice. This complexity manifests in the instability of the optimization algorithms used in learning that fluctuate instead of converging toward a global minimum. Trying different optimization algorithms wouldn’t solve the problem, since no mathematical algorithm may fight exponential complexity, so the only solution is to reduce the complexity by renouncing to the strategy of connecting each layer with all nodes of the previous layer. Instead, for each layer we must use a topology well suited to the purpose of the functions that we expect be learned by that module.
I will use image recognition as an example to describe more complex architectures, since it is one of the most complex problems neural networks are expected to solve. However, all concepts I’ll describe may be applied completely or in part also to other domains with minor modifications.
First of all, we may reduce complexity by facing explicitly the space translation problem, that is the fact that the same pattern may appear in any part of an image. A similar problem exists also in speech recognition where we have a time translation problem.
Translation problems are easily solved by using convolutional layers:
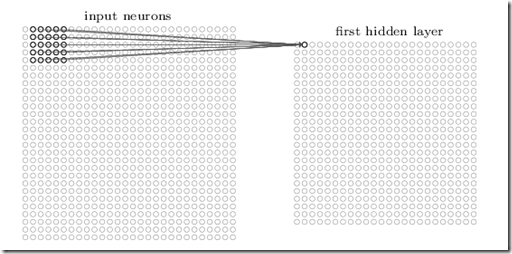
Nodes are visually organized like the pixels of the image. Each node of the convolutional layer is connected just to a small window of nodes of the previous layer around the node that has its same position in the previous layer. The purpose of this small window is to recognize an elementary pattern in that position and then to encode the strength of the match in the output value of the node of the convolutional layer.Now, since the recognition algorithm must be the same all over the image area, the weights of all connections associated to this windows are kept the same for all nodes of the convolutional layer. For the same reason all thresholds of the convolutional layer nodes are kept equal. Thus, the whole convolutionar layer must learn just a few parameters. In our picture, since the window is 5x5 all parameters are 26, (25 weights and a single thresholds). Since we don’t expect a different elementary pattern for each pixel but we expect each pattern would cover several pixels we may put a data reduction layer after the convolutional layer that just take either the maximum or the average value in a window. If the reduction window size is taken, say 4x4, we may reduce the outputs to be processed by the next layers by a factor of 16. These layers are called pooling layers, since they recognize the presence of a feature by pooling all nodes in the reduction window.
Since each convolutional layer is expected to recognize just a single elementary pattern, usually neural networks use several parallel convolutional layers, each followed by a pooling layer. Below an example architecture:
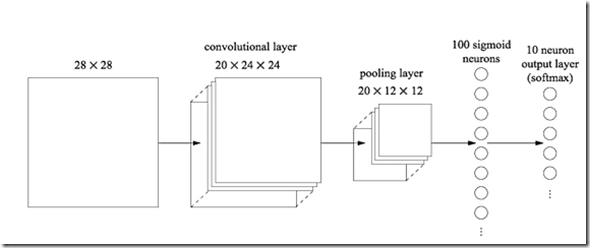
After all pooling layers a standard hidden layer whose nodes are connected with all nodes of all pooling layers, and finally an output layer whose nodes are collected as usual with all nodes of the previous layer.
Similar architectures don’t suffer of all problems of standard many-layer networks (deep networks): they are efficacious and are able to learn.
It is worth to point out that while neural networks may use techniques like convolutional layers to achieve spatial and temporal translation and and other particular techniques to adapt to the peculiarities of the situation, unlike symbolic manipulation techniques such as planning and rule based systems they don’t have general adaptation mechanism comparables to “instantiation” that was discussed in the previous section. Therefore, they are are complementary and not alternative to symbolic techniques, their main field of application being pattern recognition applied to raw data.
Learning algorithms
There are various kind of learning, that are suited for different type of applications and that complement each others. Complex systems like robots usually use several of them.
Learning to process similar inputs. The machine is trained with a training set and learns to operate also on input “similar” to the one in the training set. This is the kind of learning used in pattern recognition. Typical examples of patterns together with the expected outputs are used to train the machine. After that the machine is expected to recognize also “similar” patterns. Neural networks performs great with this kind of learning. Neural network learning is achieved by computing the network parameters that minimize a cost function on the training set with classical mathematical optimization tools. The cost function usually measures the error between the actual output provided with each training pattern and the one computed by the network. A typical measure is the average of the the squares of all output errors, but other cost functions are used to improve the convergence of the optimization algorithms. The kind of learning described in this point is the only one used with neural networks, since all other kind of learning that I am going to describe require complex symbolic manipulations and variable instantiations, that as discussed in the previous section, can’t be achieved easily with neural networks.
Learning by induction. The machine is given inputs and expected results like in the previous point, but in this case, it is expected to guess the simplest procedure that, given that inputs, produces the associated outputs.The difference with the previous point is that while in the previous point we expect a kind of interpolation in this case the machine looks for powerful extrapolations, that is, for a rule that would work also on very different inputs. Typically, guessed rules are verified on test data, that are quite different from the training set. Normally, the procedure the machine looks for, solves a well defined problem in a domain of knowledge, and good guesses are possible only if the machine has an a priori knowledge of that domain that it may use to assemble the procedure from adequate building blocks. An example of induction problem is the sequence: (1, 1), (2. 4), (3, 9), (4, 16)…..In this case the knowledge domain is number theory and the building blocks are the elementary operations. Given this a priori knowledge it is easy for an human to make an acceptable guess; the square function. Typically, during usual machine operation, where guessed procedures are used in problem solving tasks, if the machine discovers an incongruence, it automatically re-computes a new guess. Belief revision systems are useful to “patch” the reasoning chain used to guess the procedure.
Learning by analogy or by transforming the representation space. At moment this kind of learning is not used in commercial systems, but is just object of research. Basically, problem solving rules (like the one of a rule based system, for instance) are inferred from a complete different body of knowledge by building a kind of map between the two domains. Machines may also create a completely new “problem solving domain” where “problem solving” rules become trivial, or easier to guess by applying mappings to the actual problem solving domain .
Discovery has similarities with induction, but while induction requires several examples in the training set, the initial guess of a discovery may be triggered by a single example. Namely, usually we have a problem solver that performs its job while other “learning” modules watch its operation. When a learning “module” find a set of operations performed by the problem solver is “interesting” it try to assemble a new problem solving rule by combining this set of operations. Then this rule is tried in actual problem solving, and if it prove to be useful its score increases, otherwise its score go down, till the rule is removed. As an example suppose that a problem solver computes indefinite integrals. If a set of operations smartly solve an integral, it is analyzed to verify if it may be generalized also to different situations (this is quite easy to do by analyzing how problem solver rules were instantiated). If this is the case a new “integration rule” is created. Discovery has applications in automatic calculus systems and in robotics.
Conclusions
As a conclusion the main benefit we might expect from the Artificial Intelligence offer of the main clouds is the application of neural network and statistical computation to big amounts of data, since neural networks may take full advantage of SIMD massive computational power offered by the cloud, both in their normal operation and for their learning. Moreover, one may take advantage of neural networks and statistical processors that have been trained with data provided by thousands or millions of other users, thus using the cloud as a platform to cooperate with other users to get better “learning”.
Applications include data analysis based on recognition and learning of recurrent patterns. Obviously, you can’t get miracles, data must have the right format, and be quite “clean”: it is just pattern recognition, not an human analyzing and thinking about each single datum provided. Offers may include also subsequent processing of data with rule based systems to get either “advices” or “higher level” interpretation of data.
Offers include also image recognition and speech recognition services already working or needing the neural network be trained. You may also train neural networks to give simple answers to user written questions. More specifically one may automatically process a written FAQ list to get an automatic question answering systems. You should not expect a perfect virtual assistant, but something that performs a raw “keywords” and “intentions” recognition in user questions to select automatically the relevant “FAQ answer” in most of cases (80-90%).
For sure, with the passing of time always more third parties will offer SAAS services based on the various AI techniques I listed in this post. However, keep in mind, that, at moment, the only technologies, that may take full advantage of cloud massive parallelism are neural networks and statistical computations. All other offers, will take advantage just of the SAAS model, and scalability offered by the cloud.
Where to go from here?
The most famous book where to study the “basics” of artificial intelligence is with no doubt: Nilsson, “Principles of Artificial Intelligence". There, you may find the basics of all techniques discussed in this post but neural networks, and further references. A lot of intros and articles about neural networks may be easily found in the net, a good starting point being Wikipedia definition.
If you you want to learn more on Data Science and Big Data you may attend the free Microsoft courses on that subjects:


Tags: Neural Networks, Big Data, Cloud, Arificial Intelligence